Czy są w Układzie Słonecznym takie miejsca, że siła mięśni wystarczyłaby do osiągnięcia prędkości ucieczki? Czy są księżyce z których można by “zeskoczyć” na planetę wokół której krążą? Jak to policzyć? Wiele notek na tym blogu powstaje dlatego, że zadałem sobie jakieś pytanie albo coś mnie zaciekawiło. To jedna z nich.
Nie ja jeden się nad tym zastanawiałem. W sieci jest sporo różnych odpowiedzi, ale większość z nich mnie nie satysfakcjonuje, bo dokonuje zbytnich moim zdaniem uproszczeń lub podchodzi do zagadnienia w nieprzekonujący mnie sposób. Dlatego postanowiłem pokombinować samemu. Jak zobaczycie (jeśli nie przeskoczycie Strasznych Wzorów), ja też zabrałem się do tego trochę od dupy strony i też zdecydowałem się na pewne uproszczenia. Ale jedną z metod uzyskania odpowiedzi w internecie jest nie zadanie pytania ale udzielenie złej odpowiedzi - wtedy niezawodnie ktoś cię poprawi. Zatem do dzieła...
Podejście
Nie przekonuje mnie przekładanie prędkości biegu na Ziemi na inne ciała niebieskie. Osiągi Usaina Bolta trudno przełożyć na sytuację, gdzie każdy krok w jego biegu dzieliłyby długie sekundy lub nawet minuty (gdyż “dryfowałby” między kolejnymi krokami jak astronauci programu Apollo). Chciałem skupić się na sile z jaką może skoczyć lekkoatleta lub przeciętny człowiek, ale jak zwykle diabeł tkwi w szczegółach i samo obliczenie siły ludzkich nóg jest dość trudne.
W końcu jednak znalazłem świetny artykuł opisujący fizykę skoku wzwyż. Doskonale rozkłada go na czynniki pierwsze, są wykresy, wzory i mechanika kryjąca się za każdym etapem skoku. Ba, pod koniec autorzy nawet zastanawiają się jak wysoko mógłby skoczyć Michael Jordan, gdyby postawić go na Księżycu. Ale nawet oni w tak drobiazgowym artykule w tym punkcie poszli troszkę na łatwiznę. To jednak ich artykuł stał się fundamentem tej notki, więc jeśli nie straszne są Wam proste całki i trochę fizyki, to zapraszam do tekstu The Physics of the Vertical Jump.
Straszne Wzory (można przeskoczyć)
Interesuje mnie prędkość skoku, którą docelowo będziemy porównywać z prędkością ucieczki (pierwszą prędkością kosmiczną dla różnych obiektów w Układzie Słonecznym). Punktem wyjścia były dla mnie dwa wzory z artykułu: związek maksymalnej wysokości skoku z prędkością początkową oraz związek popędu (fizycznego) z masą i prędkością. By z nich skorzystać poczyniłem założenie, że skok trwa pół sekundy i zgooglałem, że przeciętny człowiek skacze na wysokość 46 cm (w odróżnieniu od Michaela Jordana, który skacze na przynajmniej 110 cm).
Dzięki temu uzyskuję siłę skoku. Następnie dodaję do tego siłę jako F=mg, czyli siłę potrzebną na zwalczanie grawitacji. Przyspieszenie to oczywiście g=9,81, masa to 80 kg dla przeciętnego człowieka i 98 kg dla Michaela Jordana. Teraz dysponuję całym “budżetem” siły. Mogę przejść do rzeczy. Odejmuję F=mgx dla danych ciał niebieskich (czyli siłę pożytkowaną na walkę z lokalną grawitacją, na utrzymać się na nogach) a reszty używam do wyliczenia prędkości początkowej. To porównujemy z prędkością ucieczki w danym miejscu.
Wyniki
Nikogo pewnie nie zaskoczy, że nie ma możliwości, by siłą mięśni uwolnić się z studni grawitacyjnej większych księżyców. Dopiero ciała o wymiarach rzędu kilkunastu-kilkudziesięciu kilometrów są wystarczająco lekkie, by astronauta mógł bać się, że zbyt gwałtowny krok pośle go w pustkę. Na powierzchni Phobosa, większego z dwóch księżyców Marsa, zarówno Michael Jordan jak i przeciętny Joe mogliby spektakularnie poskakać bez większych obaw. Ale na mniejszym z nich, Deimosie obaj mogliby... na przykład zeskoczyć na Marsa. Udało mi się znaleźć dwa miejsca gdzie tylko sportowiec pokroju Jordana mógłby powiedzieć “I don’t wanna live on this moon anymore”, spakować plecak i polecieć w cholerę, a osoby nie będące lekkoatletami mogłyby jedynie pozazdrościć. To Eros i Atlas. W przypadku tego pierwszego uśredniłem promień, więc możliwe, że MJ mógłby pokonać siłę grawitacji na odległych końcach podłużnego Erosa, ale nie na równiku.
Epilog
W kilku miejscach moje wyliczenia rozmijają się z danymi z Wikipedii, więc mogę być w błędzie. Ale rzędy wielkości powinny być OK. Co więcej wydaje mi się, że kilka lat temu, wykonywałem ten sam eksperyment myślowy i wyniki były podobne, choć na sto procent posługiwałem się inną metodą. Mówię to w oczekiwaniu na tych wszystkich, którzy zechcą mnie poprawić - do dzieła!
Źródła:
Is there a small enough planet or asteroid you can orbit by jumping?
The Physics of the Vertical Jump
Newtons Second Law force to accelerate jumping person
Throwing Something Into Orbit
Is there a small enough planet or asteroid you can orbit by jumping?
Could a Human reach escape velocity by jumping from the surface of Ceres?
if I jump high from Deimos' surface will I escape from it forever?
Podoba Ci się to co robię? Wpłyń na rozwój strony i zostań patronem Węglowego.
Nie ja jeden się nad tym zastanawiałem. W sieci jest sporo różnych odpowiedzi, ale większość z nich mnie nie satysfakcjonuje, bo dokonuje zbytnich moim zdaniem uproszczeń lub podchodzi do zagadnienia w nieprzekonujący mnie sposób. Dlatego postanowiłem pokombinować samemu. Jak zobaczycie (jeśli nie przeskoczycie Strasznych Wzorów), ja też zabrałem się do tego trochę od dupy strony i też zdecydowałem się na pewne uproszczenia. Ale jedną z metod uzyskania odpowiedzi w internecie jest nie zadanie pytania ale udzielenie złej odpowiedzi - wtedy niezawodnie ktoś cię poprawi. Zatem do dzieła...
Podejście
Nie przekonuje mnie przekładanie prędkości biegu na Ziemi na inne ciała niebieskie. Osiągi Usaina Bolta trudno przełożyć na sytuację, gdzie każdy krok w jego biegu dzieliłyby długie sekundy lub nawet minuty (gdyż “dryfowałby” między kolejnymi krokami jak astronauci programu Apollo). Chciałem skupić się na sile z jaką może skoczyć lekkoatleta lub przeciętny człowiek, ale jak zwykle diabeł tkwi w szczegółach i samo obliczenie siły ludzkich nóg jest dość trudne.
W końcu jednak znalazłem świetny artykuł opisujący fizykę skoku wzwyż. Doskonale rozkłada go na czynniki pierwsze, są wykresy, wzory i mechanika kryjąca się za każdym etapem skoku. Ba, pod koniec autorzy nawet zastanawiają się jak wysoko mógłby skoczyć Michael Jordan, gdyby postawić go na Księżycu. Ale nawet oni w tak drobiazgowym artykule w tym punkcie poszli troszkę na łatwiznę. To jednak ich artykuł stał się fundamentem tej notki, więc jeśli nie straszne są Wam proste całki i trochę fizyki, to zapraszam do tekstu The Physics of the Vertical Jump.
Straszne Wzory (można przeskoczyć)
Interesuje mnie prędkość skoku, którą docelowo będziemy porównywać z prędkością ucieczki (pierwszą prędkością kosmiczną dla różnych obiektów w Układzie Słonecznym). Punktem wyjścia były dla mnie dwa wzory z artykułu: związek maksymalnej wysokości skoku z prędkością początkową oraz związek popędu (fizycznego) z masą i prędkością. By z nich skorzystać poczyniłem założenie, że skok trwa pół sekundy i zgooglałem, że przeciętny człowiek skacze na wysokość 46 cm (w odróżnieniu od Michaela Jordana, który skacze na przynajmniej 110 cm).
Dzięki temu uzyskuję siłę skoku. Następnie dodaję do tego siłę jako F=mg, czyli siłę potrzebną na zwalczanie grawitacji. Przyspieszenie to oczywiście g=9,81, masa to 80 kg dla przeciętnego człowieka i 98 kg dla Michaela Jordana. Teraz dysponuję całym “budżetem” siły. Mogę przejść do rzeczy. Odejmuję F=mgx dla danych ciał niebieskich (czyli siłę pożytkowaną na walkę z lokalną grawitacją, na utrzymać się na nogach) a reszty używam do wyliczenia prędkości początkowej. To porównujemy z prędkością ucieczki w danym miejscu.
Wyniki
Nikogo pewnie nie zaskoczy, że nie ma możliwości, by siłą mięśni uwolnić się z studni grawitacyjnej większych księżyców. Dopiero ciała o wymiarach rzędu kilkunastu-kilkudziesięciu kilometrów są wystarczająco lekkie, by astronauta mógł bać się, że zbyt gwałtowny krok pośle go w pustkę. Na powierzchni Phobosa, większego z dwóch księżyców Marsa, zarówno Michael Jordan jak i przeciętny Joe mogliby spektakularnie poskakać bez większych obaw. Ale na mniejszym z nich, Deimosie obaj mogliby... na przykład zeskoczyć na Marsa. Udało mi się znaleźć dwa miejsca gdzie tylko sportowiec pokroju Jordana mógłby powiedzieć “I don’t wanna live on this moon anymore”, spakować plecak i polecieć w cholerę, a osoby nie będące lekkoatletami mogłyby jedynie pozazdrościć. To Eros i Atlas. W przypadku tego pierwszego uśredniłem promień, więc możliwe, że MJ mógłby pokonać siłę grawitacji na odległych końcach podłużnego Erosa, ale nie na równiku.
Epilog
W kilku miejscach moje wyliczenia rozmijają się z danymi z Wikipedii, więc mogę być w błędzie. Ale rzędy wielkości powinny być OK. Co więcej wydaje mi się, że kilka lat temu, wykonywałem ten sam eksperyment myślowy i wyniki były podobne, choć na sto procent posługiwałem się inną metodą. Mówię to w oczekiwaniu na tych wszystkich, którzy zechcą mnie poprawić - do dzieła!
Źródła:
Is there a small enough planet or asteroid you can orbit by jumping?
The Physics of the Vertical Jump
Newtons Second Law force to accelerate jumping person
Throwing Something Into Orbit
Is there a small enough planet or asteroid you can orbit by jumping?
Could a Human reach escape velocity by jumping from the surface of Ceres?
if I jump high from Deimos' surface will I escape from it forever?
Podoba Ci się to co robię? Wpłyń na rozwój strony i zostań patronem Węglowego.


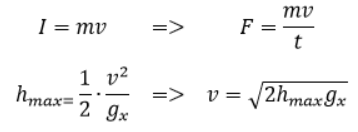


Brak komentarzy:
Prześlij komentarz